BOSS OF MATH: Polinomial

Assalamu'alaikum, teman-teman! ★
Di postingan kali ini, BOSS OF MATH akan membahas mengenai materi polinomial.
Apa sih polinomial itu? Langsung saja lihat penjelasannya dibawah ini, ya!

Pengertian Polinomial
Polinomial adalah nama lain dari suku banyak. Suku banyak (polinomial) dalam x yang berderajat n, dengan n bilangan cacah dan a_n≠0 dituliskan dalam bentuk:

dengan
1. $a_n\neq 0$
2. $n$ bilangan cacah.
3. $a_{n}$ , $a_{n-1}$ , ..., $a_2, a_{1,}a_{0}$ adalah bilangan real yang merupakan koefisien suku banyak.
4. $x^{n}, x^{n-1},...,x^2, x$ merupakan variabel.
Contoh : $5x^3 - 2x^2+4x-1$
Nilai Suku Banyak
Kita bisa mendapatkan nilai suku banyak dengan dua cara yakni :
1. Cara Substitusi
Contoh : Jika P(x) = $2x^3-x^2-2x+1,$ , tentukan P(2)
Jawab : P(-1) = $2(2)^3-(2)^2-2(2)+1$
= 2(8) - (4) - 4 + 1
= 16 -7
= 9
2. Cara Horner
Misal akan ditentukan nilai suku banyak $f(x)$ = $ax^2+bx+c$ , untuk $x=k$ maka cara horner sebagai berikut

Pembagian Polinomial dan Teorema Sisa
Pembagian suku banyak (Polinomial) dapat ditinjau sebgai pembagian bilangan bulat seperti :
112:9 mendapatkan hasil bagi 12 dan sisa 4.Hal ini bisa dituliskan:
112=9 x 12 + 4 dengan sisa (S) memenuhi $o\leq (S) < 9$

Bentuk Umum : $f(x)= P(x).H(x)+S(x)$
dimana:
f(x) = Suku Banyak
P(x) = Pembagi
H(x) = Hasil
S(x) = Sisa

Contoh :

F(x) = 2x³ – 3x² + x + 5 dibagi dengan P(x) = 2x² – x – 1

1. Pembagian Biasa

Sehingga hasil baginya: H(X) = x – 1, sisanya S(x) = x + 4

2. Cara Horner

H(x) = 1.x – 1 = x – 1

S(x) = P₁.S₂ + S₁ = (2x + 1).1/2 + 7/2 = x + ½ + 7/2 = x + 4

Teorima Faktor

Masuk ke pembahasan teorema selanjutnya yaitu teorema faktor. Inti dari teorema faktor adalah suatu pembagi merupakan faktor dari suku banyak jika memiliki sisa nol (0). Jadi, teorema sisa masih diperlukan di sini, yaitu untuk mengetahui sisa dari suatu pembagian suku banyak. Jika sisa pembagian suatu suku banyak adalah nol (0) atau tidak memiliki sisa, maka pembagi tersebut merupakan faktor dari suku banyak. Sebaliknya, jika sisanya tidak nol maka pembagi tersebut bukan merupakan faktor suku banyak.
Teorema Faktor Pada Suku Banyak

Contoh Soal: Tentukan nila a dan b $x^3 - ax^2 + 5x + b$ habis dibagi $x^2 - 2x - 3.$

Pembahasan: $x^2 - 2x - 3 = (x - 3)(x + 1)$

Disubtitusikan kedalam $x^3 - ax^2 + 5x + b = 0$

$f(3) = 3^3 - a(3)^2 + 5(3) + b = 0$

$0 = 42 - 9a + b$

$-42 = -9a + b$ ……………(1)

$f(-1) = (-1)^3 - a(-1)^2 + 5(-1) + b = 0$

$0 = -1 - a - 5 + b$

$6 = -a + b$ ……………(2)

Dari persamaan (1) dan (2) diperoleh:

$a = 6$

$b = 6 + a = 6 + 6 = 12$

Akar- Akar Suku Banyak

Akar-akar suatu suku banyak merupakan nilai yang menyebabkan suku banyak tersebut bernilai nol. Akar-akar suatu suku banyak dapat diperoleh dengan cara memfaktorkan suku banyak tersebut. Misalkan kita memiliki persamaan suku banyak sebagai berikut:

anxn + an-1xn-1 + an-2xn-2 + ….+ a2xn + a1x + ao = 0

Untuk mencari akar-akar rasional suku banyak maka kita harus bisa memfaktorkannya. Ada beberapa cara yang dapat membantu kita untuk memfaktorkan suku banyak, yaitu :

Jika ao= 0 maka salah satu akar suku banyak adalah 0.
Jika jumlah koefisisen suku banyak adalah 0 maka satu akar suku banyak adalah 1 (suku banyak bisa dibagi x – 1)
Jika jumlah koefisien x yang berpangkat genap sama denga jumlah koefisin x yang berpangkat ganjil maka satu akar suku banyak adalah -1 (suku banyak bisa dibagi x + 1)

Menentukan Faktor-Faktor Suatu Suku Banyak:

Langkah 1

Jika (x – k) adalah faktor dari suku banyak f(x) = anxn + an-1xn-1 + … + a2x2 + a1x + a0 maka nilai-nilai k yang mungkin adalah nilai faktor-faktor bulat dari a0.

Langkah 2

Dengan cara coba-coba, substitusikan nilai x = k sehingga diperoleh f(x) = 0. Jika demikian maka (x – k) adalah faktor dari f(x). Akan tetapi jika f(k) ≠ 0 maka (x – k) bukan faktor dari f(x).

Langkah 3

Setelah dipeeroleh sebuah faktor (x – k), faktor-faktor yang lain dapat ditentukan dari suku banyak hasil bagi f(x) oleh (x – k).

Sifat Akar-akar Suku Banyak

Pada persamaan berderajat 3:

ax3 + bx2 + cx + d = 0 akan mempunyai akar-akar x1, x2, x3

dengan sifat-sifat:

Jumlah 1 akar: x1 + x2 + x3 = – b/a
Jumlah 2 akar: x1.x2 + x1.x3 + x2.x3 = c/a
Hasil kali 3 akar: x1.x2.x3 = – d/a

Pada persamaan berderajat 4:

ax4 + bx3 + cx2 + dx + e = 0 akan mempunyai akar-akar x1, x2, x3, x4

dengan sifat-sifat:

Jumlah 1 akar: x1 + x2 + x3 + x4 = – b/a
Jumlah 2 akar: x1.x2 + x1.x3 + x1.x4 + x2.x3 + x2.x4 + x3.x4 = c/a
Jumlah 3 akar: x1.x2.x3 + x1.x2.x4 + x2.x3.x4 = – d/a
Hasil kali 4 akar: x1.x2.x3.x4 = e/a

Dari kedua persamaan tersebut, kita dapat menurunkan rumus yang sama untuk persamaan berderajat 5 dan seterusnya

(amati pola: –b/a, c/a, –d/a , e/a, …)

Contoh Soal :

Diberikan persamaan 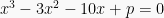$x^3 - 3x^2 - 10x + p = 0$ dengan akar-akarnya 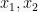$x_1,x_2$ dan

$x_3$ . Jika $2x_1 = -x -x_3$ . Carilah nilai p dan akar-akarnya.

Pembahasan

$2x_1 = -x_2 - x_3 = -(x_2 +x_3)$

Maka:

$x_1 + x_2 +x_3 = -\frac{b}{a}$

$x_1 - 2x_1 = -\frac{b}{a}$

$x_1 = \frac{b}{a} = \frac{-3}{1} = -3$

Kemudian disubstitusi dalam persamaan suku banyak:

$x^3 - 3x^2 - 10x + p = 0$

$(-3)^3 - 3(-3)^2 - 10(-3) + p = 0$

$-27 -27 + 30 + p = 0$

$p = 24$

Kemudian persamaan menjadi:

$x^3 - 3x^2 - 10x + 24 = 0$

Jika dibagi $(x+ 3)$ menjadi:

$(x+ 3)(x^2 - 6x + 8) = 0$

$(x + 3)(x - 2)(x - 4) = 0$

Sehingga:

$x_1 = -3$

$x_2 = 2$

$x_3 = 4$

$p = 24$

Fungsi Pecahan Sebagian

Diketahui

f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + a_{n - 2} x^{n - 2} + ... + a_{1} x + a_{o}

dan g(x)=

g (x) = b_{n} x^{n} + b_{n - 1} x^{n - 1} + b_{n - 2} x^{n - 2} + ... + b_{1} x + b_{o}

Jika

f (x) = g (x)

maka

a_{i} = b_{i}

untuk

i = 1, 2, 3, ..., n

Bentu k kesamaan untuk pecahan suku banyak :

Jika penyebut bisa difaktorkan dan derajat pembilang lebih kecil dari derajat penyebut:

Misalkan

l (x)

adalah factor linier,

l (x) = ax + b

k (x)

adalah factor bentuk fungsi kuadrat,

k (x) = p x^{2} + qx + r

t (x)

adalah factor bentuk fungsi pangkat tiga,

t (x) = c x^{3} + d x^{2} + ex + f

maka sebagai ilustrasi :

(1)

\frac{P (x)}{l_{1} (x) \times l_{2} (x) \times ...} = \frac{a}{l_{1} (x)} + \frac{b}{l_{2} (x)} + ...

Contoh :

\frac{2 x + 5}{x^{2} - x - 2} = \frac{2 x + 5}{(x - 2) (x + 1)} = \frac{3}{x - 2} + \frac{- 1}{x + 1}

(2)

\frac{P (x)}{l_{1} (x) \times {\{l_{2} (x)\}}^{2} \times ...} = \frac{a}{l_{1} (x)} + \frac{b}{l_{2} (x)} + \frac{cx + d}{{(l_{2} (x))}^{2}} + ...

( memuat factor linier berulang)

Contoh :

\frac{4 x^{2} + 7 x + 7}{(x - 1) {(x + 2)}^{2}} = \frac{2}{x - 1} + \frac{1}{x + 2} + \frac{x - 1}{{(x + 2)}^{2}}

(3)

\frac{P (x)}{l (x) \times k (x) \times t (x) ...} = \frac{a_{1}}{l (x)} + \frac{a_{2} x + a_{3}}{k (x)} + \frac{a_{4} x^{2} + a_{5} x + a_{6}}{t (x)} + ...

Contoh Soal: Tentukan nilai a,,b,c pada kesamaan

\frac{6 x}{x^{2} + 4 x + 3} = \frac{a}{x + 1} + \frac{b}{x + 2}

\frac{6 x}{x^{2} + 4 x + 3} = \frac{a}{x + 1} + \frac{b}{x + 2}

= \frac{a (x + 2) + b (x + 1)}{(x + 1) (x + 2)}

= \frac{(a + b) x + 2 a + b}{x^{2} + 4 x + 3}

Selanjutnya dengan menyamakan koefisien dari pembilang di kedua ruas didapat :

Koefisien

x

pembilang

\to

6 = a + b

(1)

Suku konstan dari pembilang

\to

0 = 2 a + b

(2)

Dengan mengeliminasi kedua persamaan didapat :

a = - 6

dan

b = 12

Jadi

\frac{6 x}{x^{2} + 4 x + 3} = \frac{- 6}{x + 1} + \frac{12}{x + 2}

DAFTAR PUSTAKA

Noormandiri, BK. 2017. Kelompok Peminatan Matematika dan Ilmu-Ilmu Alam. Jakarta : UHAMKA

Tim Presiden Eduka. 2016. Top Sukses Matematika. Surabaya

B.K. Noormandiri. 2017. Matematika Kelompok Peminatan untuk SMA Kelas XI. Jakarta: Erlanggaa

Frank Ayres Jr. Philip A., Schmidt. 2004. Schaum's Outline of Theory and Problems of College

Nama Anggota Kelompok
Hanna Virdya Sabilillah
Syarif Muhammad Azdi Razi
Veren Pramestya Anantasa

BOSS OF MATH

Monday, 13 May 2019

Polinomial

0 comments:

Post a Comment

About Me

Archive

Search This Blog

Report Abuse

Pages

Seguidores